
When I cheerfully announced to my Year 4 class at the end of a Maths lesson that we would be starting fractions next week, it’s safe to say that their reaction was rather… lacklustre. This piece of information was met with groans, a few theatrical gasps and so many nervous glances around at their peers that you’d think I’d just announced the not-so-untimely demise of TikTok. Alas, all it took was the very mention of the word ‘fraction’ to strike fear, trepidation and teenager-like sullenness into the hearts of my usually enthusiastic 8-9 year olds. Funnily enough, I’m sure I would have received a very similar reaction had I made the same announcement in the staff room at lunchtime. In fact, upon realising that fractions were fast approaching when discussing planning with a colleague, my own reaction was not dissimilar. This led me to ask myself why teachers and pupils alike often have a less positive attitude towards fractions than other areas of Maths and, put simply, it is this: fractions are HARD.
Let us start by examining the fraction knowledge that all children are expected to be equipped with by the end of primary school. In EYFS, doubles facts set children up very nicely to begin learning about halves and quarters in Year 1. From there, children should finish Key Stage 1 by learning about thirds, finding simple fractions of amounts and recording these, as well as getting their first taste of equivalent fractions in the form of one half being equivalent to two quarters. In Lower Key Stage 2, tenths are introduced, we distinguish between unit and non-unit fractions and we begin to add and subtract fractions with the same denominator. By the time children finish their Upper Key Stage 2 journey, they are expected to have a robust knowledge of equivalent fractions, converting between improper fractions and mixed numbers, and the four operations involving fractions to name just a few key points. It is clear that the curriculum is designed to be sequential and build up knowledge in small steps as recommended by Rosenshine (2012). So, the question still remains: what makes fractions so difficult?
As a Maths subject leader and an experienced teacher that has worked across both KS1 and KS2, these are some of the key factors that I believe contribute heavily to children’s difficulties in understanding fractions, creating a negative stigma which for many of us lasts into adulthood.
- An abstract concept: Coming from a world of counting, adding and subtracting only using whole numbers makes it very difficult for children to understand the concept of one of these numbers (or an object/item/group/quantity) being split into equal parts that can come back together to make the whole. This is especially true when we start introducing equivalent fractions, decimal and percentage equivalents and the four operations involving fractions. When calculating using fractions with different denominators, we can see must be very confusing from a child’s perspective. It is no stranger than handing them an apple and an orange and telling them to add them together, but in order to do that you need to turn them both into bananas but remembering that they’re actually still apples and oranges. Maybe we’ll even have to give our answer in pears.
- Insecure existing knowledge: In a recent conversation, a colleague pointed out that when it comes to equivalent fractions, if children do not have sound times table knowledge then they are already starting on the back foot. An excellent point, well made. In fact, this applies not only to equivalent fractions but to fractions overall. When asking a child to find three sevenths of a quantity, they must have a very robust knowledge of the 7 times table to be able to do this mentally.
- The concept of the whole: We suddenly start referring to the numbers that children are familiar with as “whole numbers” and emphasising the words part and whole. However, 6 is the whole. 39 is the whole. 1453 is the whole. The idea that “the whole” refers to anything that we are sharing into equal parts, that the whole is what we get when we have all of our equal parts together, is a truly overwhelming concept that must be tackled with caution and precision.
- What’s the top number called again, Miss? When children encounter written fractions, they see familiar numbers but represented in an unfamiliar form. All of a sudden, they are balancing on top of each other as if they are performing some sort of circus act. They have taken on new names (No, no, no! It’s a denominator, NOT a dementor, although I do enjoy the Harry Potter reference!) and it can take some time to help children understand the role of each part of a written fraction.
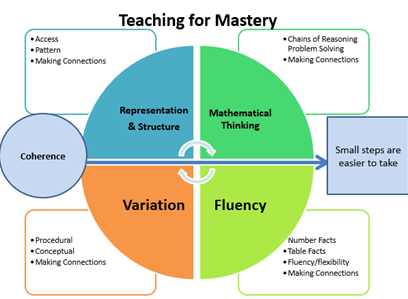
- Visual representations: I know that a pet peeve of another colleague of mine is to see fractions always visually represented as a pizza or a cake. We have such a tendency to veer toward circular representations, but why? They are infinitely more difficult for children to independently construct to support them in their own learning, and children become reliant on a single representation. As the diagram below suggests, (NCETM, 2017) variation linked with visual representation and structure is essential in teaching for mastery.
- Vocabulary: This point is not specific to fractions, and links with my earlier point about the names of different parts of a written fraction. As with any new area of mathematics, fractions bring a whole host of new vocabulary that children need to grapple with. Fourteen thirds
 is an improper fraction, but also a non-unit fraction at the same time. All unit fractions are proper fractions, but not all non-unit fractions are improper fractions. Essential? Yes. Bewildering? Also, yes.
is an improper fraction, but also a non-unit fraction at the same time. All unit fractions are proper fractions, but not all non-unit fractions are improper fractions. Essential? Yes. Bewildering? Also, yes.
So just how do we go about making this particular area of mathematics a bit more traversable?
- Scaffold, scaffold, scaffold: We all know that the focus in education has shifted hugely from differentiation to scaffolding. This could be as simple as a child with poor times table knowledge having access to a multiplication square that you have modelled how to use, providing an ‘I do, we do, you do’ style of modelling and leaving your models available throughout the lesson for children to refer back to, or providing concrete resources which brings me on to…
- Manipulatives: Manipulatives are absolutely your friend when teaching fractions. It is, without a doubt, one of the areas of Mathematics that best lends itself to the use of practical resources. Numicon, base 10, fraction walls and even the humble but versatile multilink cube have a very valuable place in supporting with fractions teaching.
- Varied visual representation: As mentioned above, varying the ways in which you present Mathematical content support pupils in their mastery of the curriculum. This is not to say that when you get down to the nitty gritty, you should have 5 different diagrams for every problem (I am personally a fan of a simple bar model), but ensure that pupils are exposed to the different visuals available throughout your focus on fractions to allow them to spot patterns and make links.
- Ask them! If in doubt, talk it out. As we all know, pupils sometimes struggle to articulate their difficulties as they are often unaware of exactly what it is that they are finding difficult in the first place, but in encouraging pupils to try and explain rather than accepting “I’m stuck.”, we can help to build metacognitive skills by making them aware of their own learning and we can model this thought process for our pupils. “I can see that you have added the two numerators perfectly. I think what you have found tricky is…? Does that sound right? Let’s do an example together.”

Well, we’ve come to the end of my musings and I hope that you’ve found some ideas that resonate with you, some strategies to try or even just some comfort in the fact that someone else feels the same way about teaching fractions. To finish, when I did some research for this article I came across a poster (pictured) which gave me a small chuckle, but what gave me an even bigger chuckle was the website that this poster is sold on (youthchg.com) which describes it as “your best bet to overcome all the obstacles to math instruction that your students present”. Despite that compelling product description, I would like to emphasise that the landscape of teaching fractions is not so hopeless and barren that you should just slap a poster on your classroom wall and hope for the best. Instead, know your pupils and guide them through this tricky but essential area of Mathematics with scaffolding, discussion, care and the patience of a saint.
Frankie Barrington, Oakley Vale Primary School
References:
NCETM (2017) Five Big Ideas in Teaching for Mastery. Available at: Five Big Ideas in Teaching for Mastery | NCETM (Accessed: 17/2/2022)
Rosenshine, B. (2012) Principles of Instruction. American Educator. Spring 2012. pp12-39.
Youthchg. (year unknown) Poster #328. Available at: Poster #328 - Fractions, Arithmetic, Math Poster for Middle, High School Classrooms - Youth Change (youthchg.com) (17/2/2022)

